面试-算法

面试 Comments 
1
主要总结算法的模板题

1. 输入输出

1
2
3
常用的数据输入方法有两种，Scanner和BufferedReader。
BufferedReader可以读一行，速度比Scanner快，所以数据较多的时候使用。
注意BufferedReader用完记得关。

1.1 输入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
// 1. 导入包
import java.io.*;
 
public class Main{
    //2. 抛出IOException异常
    public static void main(String[] args) throws IOException {
        // 3. 定义BufferedReader类
        // 最后不要忘了关闭reader
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

        /**
         * 字符串
         */
        // 只读取一行字符串
        String string1 = reader.readLine();
        // 连续读取多行字符串
        String string2;
        while((str = reader.readLine()) != null){
            //如果不为空，才进行下述操作
            System.out.println(string2);
        }

        /**
         * char
         */
        // 一行一个char
        char ca = reader.readLine().charAt(0);
        // 一行一个char数组
        char[] charArray = reader.readLine().toCharArray();

        /**
         * 整型
         */
        // 一行一个整数
        short short1 = Short.parseShort(reader.readLine());
        int int1 = Integer.parseInt(reader.readLine());
        long long1 = Long.parseLong(reader.readLine());
        // 一行多个整数
        String[] sList = reader.readLine().split(" "); //用空格分割，也可以用逗号分割
        for (String s : sList){
            // String转为整数
            System.out.println(Integer.parseInt(s));
        }
        // 转化为int数组
        int[] arr = new int[s.length];
        for(int i = 0; i < s.length; i++){
            arr[i] = Integer.parseInt(s[i]);
        }

        /**
         * 浮点型
         */
        // float
        float f = Float.parseFloat(reader.readLine());
        // double
        double d = Double.parseDouble(reader.readLine());

        /**
         * 大数
         */
        BigInteger bigInteger1 = new BigInteger(reader.readLine());
        BigInteger bigInteger2 = new BigInteger(reader.readLine());
        // 加
        System.out.println(bigInteger1.add(bigInteger2));
        // 减 
        System.out.println(bigInteger1.subtract(bigInteger2));
        // 乘
        System.out.println(bigInteger1.multiply(bigInteger2));
        // 除
        System.out.println(bigInteger1.divide(bigInteger2));

        /**
         * 高精度浮点数
         */
        BigDecimal bigDecimal1 = new BigDecimal(reader.readLine());
        BigDecimal bigDecimal2 = new BigDecimal(reader.readLine());
        // 加
        System.out.println(bigDecimal1.add(bigDecimal2));
        // 减
        System.out.println(bigDecimal1.subtract(bigDecimal2));
        // 乘
        System.out.println(bigDecimal1.multiply(bigDecimal2));
        // 除
        System.out.println(bigDecimal1.divide(bigDecimal2, 3, RoundingMode.HALF_UP)); // 第二个参数：保留小数位数；第三位参数：四舍五入模式

        /**
         * 进制
         */
        // 字符串转2进制int
        int int2 = Integer.parseInt(reader.readLine(), 2);
        // 字符串转2进制大数
        BigInteger bigInteger2 = new BigInteger(reader.readLine(), 2);

        /**
         * double格式化
         */
        // 导入包：import java.text.*;
        NumberFormat formatter;
        String s;
        double d = -1234.567;
        // 强制在整数部分加0：0，多几位就多几个0
        formatter = new DecimalFormat("000000");
        s = formatter.format(d);
        System.out.println(s);                  // -001235
        formatter = new DecimalFormat("00");
        s = formatter.format(d);
        System.out.println(s);                  // -1235
        // 强制保留小数部分：0，有几个0就保留几位小数
        formatter = new DecimalFormat("000000.00");
        s = formatter.format(d);
        System.out.println(s);                  // -001235.57
        formatter = new DecimalFormat(".00");
        s = formatter.format(d);
        System.out.println(s);                  // -1235.57

        /**
         * 排序
         */
        System.out.println("array默认升序_________________________________________________");
        //默认升序，从小到大
        int[] arr = {1,3,8,5,2,7};
        Arrays.sort(arr);
        System.out.println(Arrays.toString(arr));
        System.out.println("array降序_______________________________________________");
        Integer[] arr2 = new Integer[]{1,2,3,8,5};
        // 只支持包装类元素逆序
        Arrays.sort(arr2,Collections.reverseOrder());
        System.out.println(Arrays.toString(arr2));

        System.out.println("List默认升序_______________________________________________");
        List<Integer> arrList = new ArrayList<>();
        arrList.add(1);arrList.add(4);arrList.add(2);arrList.add(78);arrList.add(23);
        //集合工具类Collections，对集合进行升序排序
        Collections.sort(arrList);
        System.out.println(Arrays.toString(arrList.toArray()));
        System.out.println("List降序__________________________________________________");
        Collections.sort(arrList,Collections.reverseOrder());
        System.out.println(Arrays.toString(arrList.toArray()));
        
        // 关闭reader
        reader.close();
    }
}

1.2 输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 1. 单行输出
System.out.println(result);

// 2. 多行输出
System.out.println(result1);
System.out.println(result2);
System.out.println(result3);

// 3. 格式化输出
System.out.printf("Formatted result: %.2f", floatValue);

// 4. 输出数组或集合
int[] array = {1, 2, 3, 4, 5};
for (int num : array) {
    System.out.print(num + " ");
}

// 5. 特殊字符输出
System.out.println("Line 1\nLine 2\tTabbed");


2. 排序算法

2.1 分类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
graph LR;
A(排序) --> B(内部排序)
A(排序) --> C(外部排序)

B --> D(选择排序)
B --> E(插入排序)
B --> F(交换排序)
B --> G(归并排序)
B --> H(桶排序)

C --> I(多路归并)
C --> J(败者树)

D --> K(直接选择排序)
D --> L(堆排序)

E --> M(直接插入排序)
E --> N(希尔排序)

F --> O(冒泡排序)
F --> P(快速排序)

H --> Q(计数排序)
H --> R(基数排序)

2.2 时间复杂度和空间复杂度

排序算法平均时间复杂度最坏时间复杂度最好时间复杂度空间复杂度稳定性
冒泡排序O(n2)O(n2)O(n)O(1)稳定
直接选择排序O(n2)O(n2)O(n)O(1)不稳定
直接插入排序O(n2)O(n2)O(n)O(1)稳定
快速排序O(nlogn)O(n2)O(nlogn)O(logn)不稳定
堆排序O(nlogn)O(nlogn)O(nlogn)O(1)不稳定
希尔排序O(nlogn)O(ns)O(n)O(1)不稳定
归并排序O(nlogn)O(nlogn)O(nlogn)O(n)稳定
计数排序O(n+k)O(n+k)O(n+k)O(n+k)稳定
基数排序O(N*M)O(N*M)O(N*M)O(M)稳定

注：基数排序: 基数排序时间复杂度为O(N*M)，其中N为数据个数，M为数据位数。

记忆：

  • 时间复杂度：
    • 冒泡、选择、插入排序需要两个for循环，每次只关注一个元素，平均时间复杂度为O(n²)）（一遍找元素O(n)，一遍找位置O(n)）
    • 快速、堆、希尔、归并基于二分思想，log以2为底，平均时间复杂度为O(nlogn)（一遍找元素O(n)，一遍找位置O(logn)）
  • 稳定性：
    • “快希选堆”（快牺牲稳定性）
    • 排序算法的稳定性：排序前后相同元素的相对位置不变，则称排序算法是稳定的；否则排序算法是不稳定的。

2.3 原理

  • 冒泡排序

    • 原理：从数组最左端开始向右遍历，依次比较相邻元素大小，如果”左元素 > 右元素”就交换它俩。遍历完成后，最大的元素会被移动到数组的最右端。
    • 算法流程：
      • 首先，对n个元素执行”冒泡”，将数组的最大元素交换至正确位置，
      • 接下来，对剩余n-1个元素执行”冒泡”，将第二大元素交换至正确位置。
      • 以此类推，经过n-1轮”冒泡”后，前n-1大的元素都被交换至正确位置。
      • 仅剩的一个元素必定是最小元素，无须排序，因此数组排序完成。
    • 图示：
    • 代码：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      /* 冒泡排序 */
      void bubbleSort(int[] nums) {
          // 外循环：未排序区间为 [0, i]
          for (int i = nums.length - 1; i > 0; i--) {
              // 内循环：将未排序区间 [0, i] 中的最大元素交换至该区间的最右端 
              for (int j = 0; j < i; j++) {
                  if (nums[j] > nums[j + 1]) {
                      // 交换 nums[j] 与 nums[j + 1]
                      int tmp = nums[j];
                      nums[j] = nums[j + 1];
                      nums[j + 1] = tmp;
                  }
              }
          }
      }

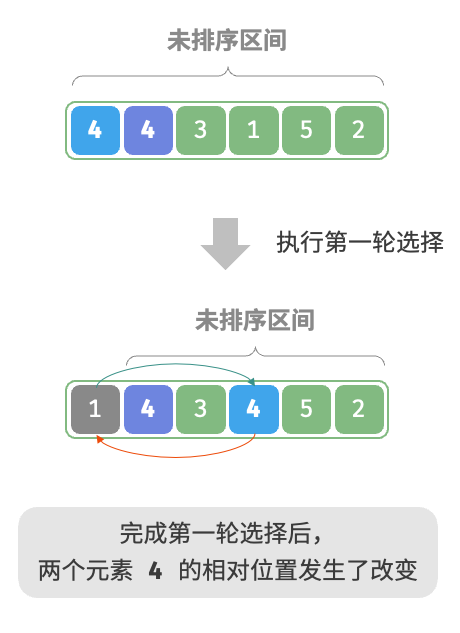
  • 选择排序：

    • 原理：轮从未排序区间选择最小的元素，将其放到已排序区间的末尾。
    • 算法流程：
      • 初始状态下，所有元素未排序，即未排序（索引）区间为[0,n-1]。
      • 选取区间[0,n-1]中的最小元素，将其与索引0处元素交换。完成后，数组前1个元素已排序。
      • 选取区间[1,n-1]中的最小元素，将其与索引1处元素交换。完成后，数组前2个元素已排序。
      • 以此类推。经过n-1轮选择与交换后，数组前n-1个元素已排序。
      • 仅剩的一个元素必定是最大元素，无须排序，因此数组排序完成。
    • 图示：
    • 代码：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      /* 选择排序 */
      void selectionSort(int[] nums) {
          int n = nums.length;
          // 外循环：未排序区间为 [i, n-1]
          for (int i = 0; i < n - 1; i++) {
              // 内循环：找到未排序区间内的最小元素
              int k = i;
              for (int j = i + 1; j < n; j++) {
                  if (nums[j] < nums[k])
                      k = j; // 记录最小元素的索引
              }
              // 将该最小元素与未排序区间的首个元素交换
              int temp = nums[i];
              nums[i] = nums[k];
              nums[k] = temp;
          }
      }

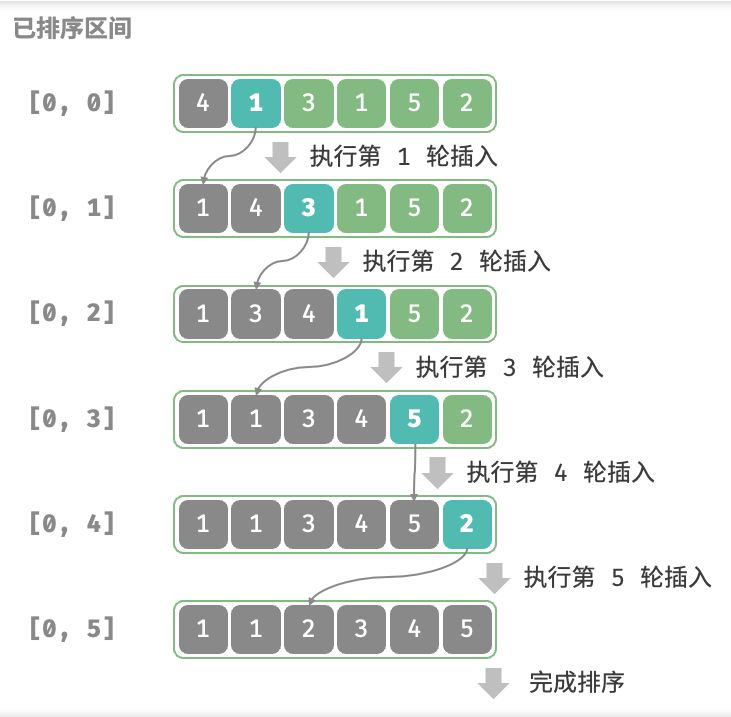
  • 插入排序

    • 原理：在未排序区间选择一个基准元素，将该元素与其左侧已排序区间的元素逐一比较大小，并将该元素插入到正确的位置。
    • 算法流程：
      • 初始状态下，数组的第1个元素已完成排序。
      • 选取数组的第2个元素作为base，将其插入到正确位置后，数组的前2个元素已排序。
      • 选取第3个元素作为base，将其插入到正确位置后，数组的前3个元素已排序。
      • 以此类推，在最后一轮中，选取最后一个元素作为base，将其插入到正确位置后，所有元素均已排序。
    • 图示：
    • 代码：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      /* 插入排序 */
      void insertionSort(int[] nums) {
          // 外循环：已排序元素数量为 1, 2, ..., n
          for (int i = 1; i < nums.length; i++) {
              int base = nums[i], j = i - 1;
              // 内循环：将 base 插入到已排序部分的正确位置
              while (j >= 0 && nums[j] > base) {
                  nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位
                  j--;
              }
              nums[j + 1] = base;        // 将 base 赋值到正确位置
          }
      }

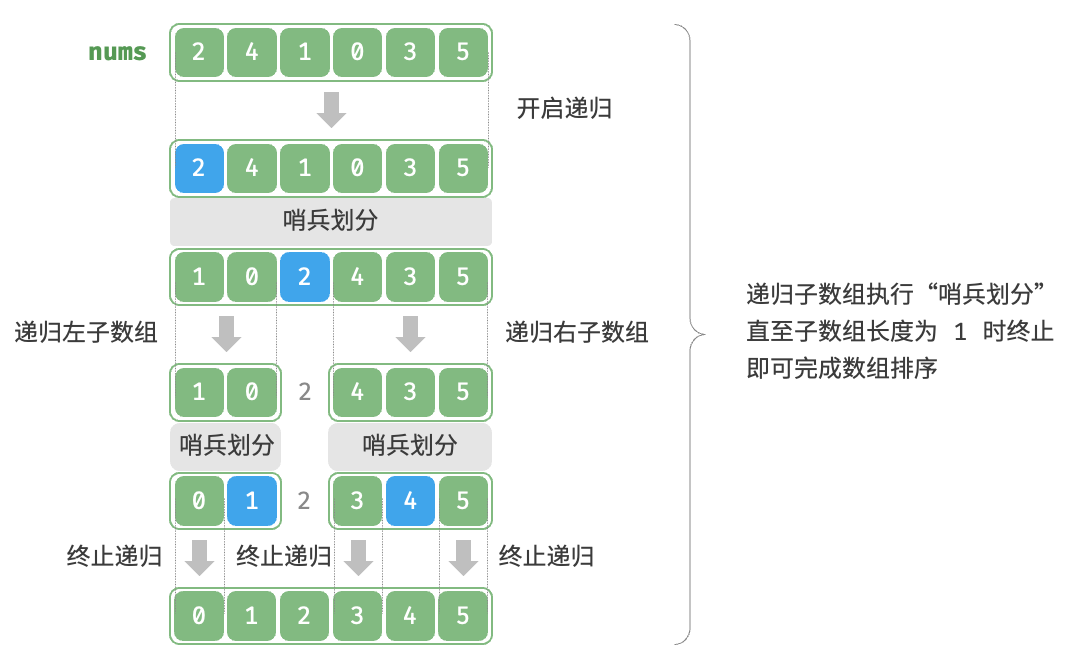
  • 快速排序：

    • 原理：选择数组中的某个元素作为“基准数”，将所有小于基准数的元素移到其左侧，而大于基准数的元素移到其右侧。
    • 算法流程：
      • 选取数组最左端元素作为基准数，初始化两个指针i和j分别指向数组的两端。
      • 设置一个循环，在每轮中使用i（j）分别寻找第一个比基准数大（小）的元素，然后交换这两个元素。
      • 循环执行步骤2，直到i和j相遇时停止，最后将基准数交换至两个子数组的分界线。
    • 图示：
    • 代码：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      /* 元素交换 */
      void swap(int[] nums, int i, int j) {
          int tmp = nums[i];
          nums[i] = nums[j];
          nums[j] = tmp;
      }

      /* 哨兵划分 */
      int partition(int[] nums, int left, int right) {
          // 以 nums[left] 作为基准数
          int i = left, j = right;
          while (i < j) {
              while (i < j && nums[j] >= nums[left])
                  j--;          // 从右向左找首个小于基准数的元素
              while (i < j && nums[i] <= nums[left])
                  i++;          // 从左向右找首个大于基准数的元素
              swap(nums, i, j); // 交换这两个元素
          }
          swap(nums, i, left);  // 将基准数交换至两子数组的分界线
          return i;             // 返回基准数的索引
      }

      /* 快速排序 */
      void quickSort(int[] nums, int left, int right) {
          // 子数组长度为 1 时终止递归
          if (left >= right)
              return;
          // 哨兵划分
          int pivot = partition(nums, left, right);
          // 递归左子数组、右子数组
          quickSort(nums, left, pivot - 1);
          quickSort(nums, pivot + 1, right);
      }

3. 链表

3.1 读取链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import java.io.*;

public class Main{
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        // 如果第一行表示节点个数，那就读取n
        int n = Integer.parseInt(reader.readLine());
        String[] s = reader.readLine().split(" "); //用空格分割，也可以用逗号分割

        // 创建虚拟头节点
        LinkNode dummy = new LinkNode(0);
        // 创建当前指针
        LinkNode current = dummy;
        for(int i = 0; i < s.length; i++){
            // 当前值
            int val = Integer.parseInt(s[i]);
            // 创建当前指针的后继
            current.next = new LinkNode(val);
            // 指针向后移一位
            current = current.next;
        }
        // current指针最后指向null
        current.next = null;
        // head指针为虚拟头节点的直接后继
        LinkNode head = dummy.next;

        // 输出链表，仅为演示，实际问题中可能要根据题目要求进行输出
        LinkNode node = head;
        while (node != null) {
            System.out.print(node.val + " ");
            node = node.next;
        }

        // 关闭资源
        reader.close();
    }

    // 辅助类：构建一个节点类，用于链表构建
    static class LinkNode {
        int val;
        LinkNode next;
        public LinkNode(int val){
            this.val = val;
        }
    }
}

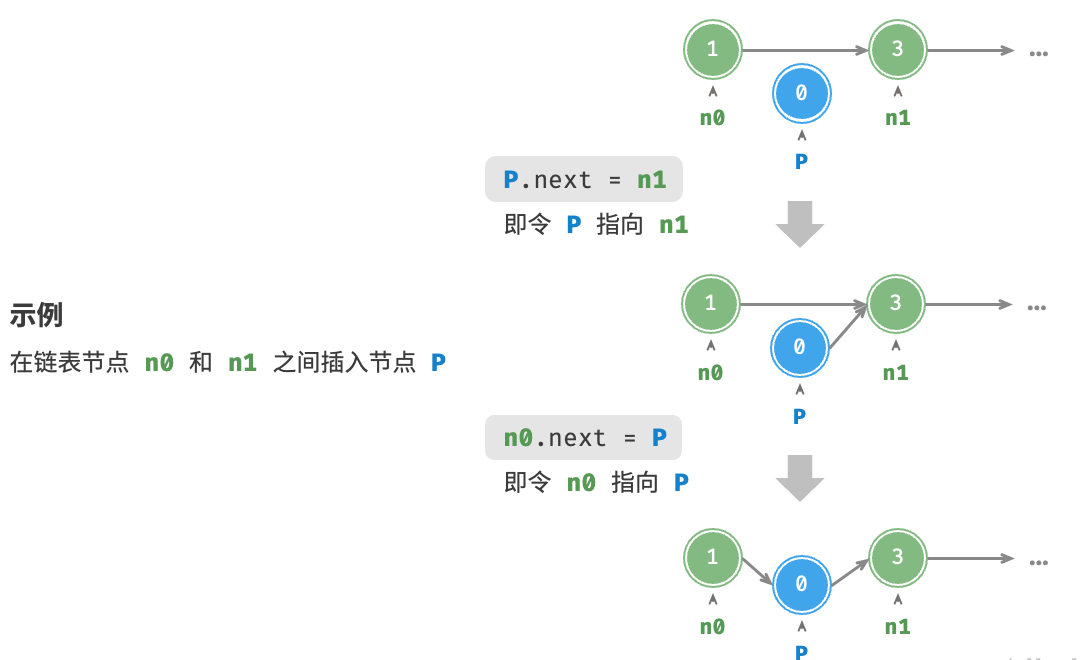
3.2 插入节点

1
2
3
4
5
6
/* 在链表的节点 n0 之后插入节点 P */
void insert(ListNode n0, ListNode P) {
    ListNode n1 = n0.next;
    P.next = n1;
    n0.next = P;
}

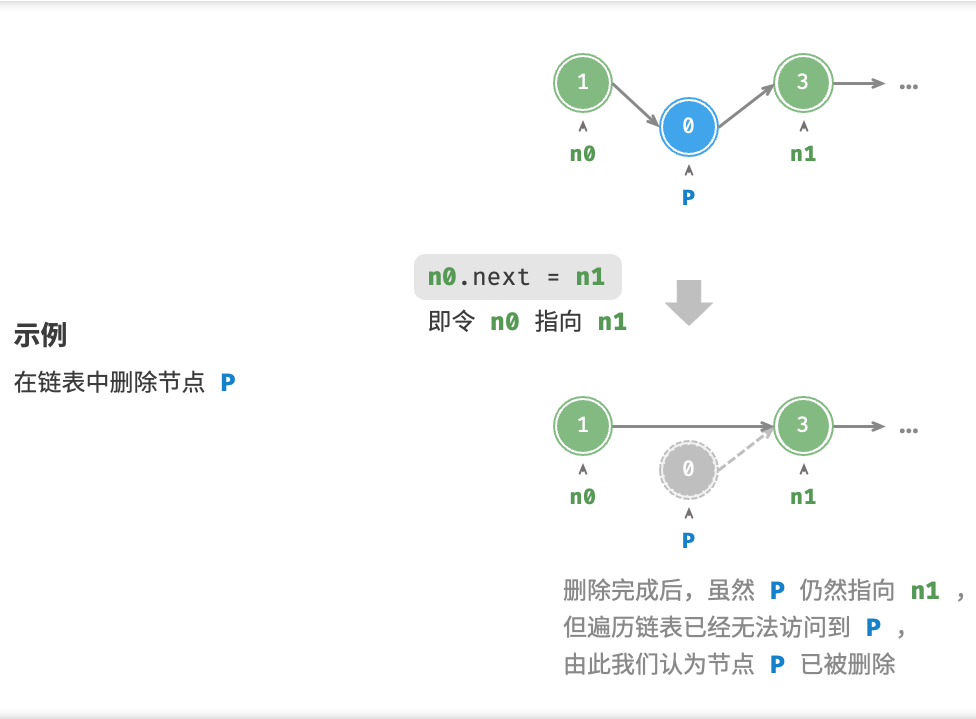
3.3 删除节点

1
2
3
4
5
6
7
8
9
10
/* 删除链表的节点 n0 之后的首个节点 */
void remove(ListNode n0) {
    if (n0.next == null)
        return;
    // n0 -> P -> n1
    // n0.next = n0.next.next;
    ListNode P = n0.next;
    ListNode n1 = P.next;
    n0.next = n1;
}

3.4 访问节点

1
2
3
4
5
6
7
8
9
/* 访问链表中索引为 index 的节点 */
ListNode access(ListNode head, int index) {
    for (int i = 0; i < index; i++) {
        if (head == null)
            return null;
        head = head.next;
    }
    return head;
}

3.5 查找节点

1
2
3
4
5
6
7
8
9
10
11
/* 在链表中查找值为 target 的首个节点 */
int find(ListNode head, int target) {
    int index = 0;
    while (head != null) {
        if (head.val == target)
            return index;
        head = head.next;
        index++;
    }
    return -1;
}

3.6 模板题

  • 移除链表元素
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    /**
     * Definition for singly-linked list.
     * public class ListNode {
     *     int val;
     *     ListNode next;
     *     ListNode() {}
     *     ListNode(int val) { this.val = val; }
     *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
     * }
     */
    class Solution {
        public ListNode removeElements(ListNode head, int val) {
            if (head == null) return head;
            // 因为删除可能涉及到头节点，所以设置dummy节点，统一操作
            ListNode dummy = new ListNode(-1, head);
            ListNode pre = dummy;
            ListNode cur = head;
            while (cur != null) {
                if (cur.val == val) {
                    pre.next = cur.next;
                } else {
                    pre = cur;
                }
                cur = cur.next;
            }
            return dummy.next;
        }
    }
  • 设计链表:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    class MyLinkedList{
        // 定义节点
        class Node{
            // 节点值
            int val;
            // 下一节点的地址
            Node next;
            // 构造器
            public Node(int val){
                this.val = val;
            }
        }
        
        // 链表的长度
        int size;
        // 虚拟头节点
        Node head;
        
        // 1、初始化链表
        public MyLinkedList(){
            size = 0;
            // 定义这个虚拟头节点的值为0
            head =  new Node(0);
        }
        
        // 2. addAtIndex方法
        public void addAtIndex(int index, int val){
            // 当index大于size
            if (index>size){
                return;
            }
            
            // 当index小于0
            if (index<0){
                index=0;
            }
            
            // current指针移动到index的前一个
            Node current = head;
            for (int i=0; i<index; i++){
                current = current.next;
            }
            // 插入的节点
            Node addNode = new Node(val);
            addNode.next = current.next;
            current.next = addNode;
            
            // 链表总数+1
            size++;
        }
        
        // 3. addAtHead方法
        public void addAtHead(int val){
            addAtIndex(0, val);
        }
        
        // 4. addAtTail方法
        public void addAtTail(int val){
            addAtIndex(size, val);
        }
        
        // 5. get方法
        public int get(int index){
            // 逻辑判断
            if (index<0 || index>size-1){
                return -1;
            }
            // 遍历每个节点
            Node current = head;
            for (int i=0; i<=index; i++){
                current = current.next;
            }
            return current.val;
        }
        
        // 6. deleteAtIndex方法
        public void deleteAtIndex(int index){
            // 逻辑判断
            if (index<0 || index>size-1){
                return;
            }  
          
            Node current = head;
            for (int i=0; i<index; i++){
                current = current.next;
            }
            current.next = current.next.next;
            size--;
        }
    }
  • 反转链表:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    /**
     * Definition for singly-linked list.
     * public class ListNode {
     *     int val;
     *     ListNode next;
     *     ListNode() {}
     *     ListNode(int val) { this.val = val; }
     *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
     * }
     */
    class Solution {
        public ListNode reverseList(ListNode head) {
            ListNode cur = head;
            ListNode pre = null;
            ListNode tem = null;
            while (cur!=null){
                // 保存下一个节点
                tem = cur.next;
                cur.next = pre;
                // 两个指针都往后移一位
                pre = cur;
                cur = tem;
            }
            return pre;
        }
    }
  • 两两交换链表中的节点:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    /**
     * Definition for singly-linked list.
     * public class ListNode {
     *     int val;
     *     ListNode next;
     *     ListNode() {}
     *     ListNode(int val) { this.val = val; }
     *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
     * }
     */
    class Solution {
        public ListNode swapPairs(ListNode head) {
            // 0/1个节点的情况
            if (head==null || head.next==null) return head;
            ListNode pre = head;
            ListNode cur = head.next;
            while (cur!=null){
                int tem = pre.val;
                pre.val = cur.val;
                cur.val = tem;
                if (cur.next==null || cur.next.next==null) return head;
                pre = pre.next.next;
                cur = cur.next.next;
            }
            return head;
        }
    }
  • 删除链表的倒数第N个节点:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    /**
     * Definition for singly-linked list.
     * public class ListNode {
     *     int val;
     *     ListNode next;
     *     ListNode() {}
     *     ListNode(int val) { this.val = val; }
     *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
     * }
     */
    class Solution {
        public ListNode removeNthFromEnd(ListNode head, int n) {
            // 虚拟指针
            ListNode dummy = new ListNode(0, head);
            // 双指针
            ListNode pre = dummy;
            ListNode cur = dummy;
            // current指针往前先移动n个
            for (int i=1; i<=n; i++){
                cur = cur.next;
            }
            // pre和cur同时往后移动
            while (cur.next!=null){
                cur = cur.next;
                pre = pre.next;
            }
            // 删除节点
            pre.next = pre.next.next;
            return dummy.next;
        }
    }
  • 链表相交:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    /**
     * Definition for singly-linked list.
     * public class ListNode {
     *     int val;
     *     ListNode next;
     *     ListNode(int x) {
     *         val = x;
     *         next = null;
     *     }
     * }
     */
    public class Solution {
        public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
            // 虚拟头节点
            ListNode dummyA = new ListNode(0);
            dummyA.next = headA;
            ListNode dummyB = new ListNode(0);
            dummyB.next = headB;
            // 长度
            int lenA = 0;
            int lenB = 0;

            // 计算两个链表的长度
            ListNode tmpA = dummyA;
            ListNode tmpB = dummyB;
            while (tmpA.next!=null){
                tmpA = tmpA.next;
                lenA++;
            }
            while (tmpB.next!=null){
                tmpB = tmpB.next;
                lenB++;
            }

            // 将最长的链表的指针往前移动|lenA-lenB|
            ListNode tmpA1 = dummyA;
            ListNode tmpB1 = dummyB;
            if (lenA>lenB){
                int step = lenA - lenB;
                for (int i=0; i<step; i++){
                    tmpA1 = tmpA1.next;
                }
            }else{
                int step = lenB - lenA;
                for (int i=0; i<step; i++){
                    tmpB1 = tmpB1.next;
                }
            }

            // tmpA1和tmpB1依次往后移动
            while (tmpA1!=null && tmpB1!=null){
                if (tmpA1==tmpB1){
                    return tmpA1;
                }
                tmpA1 = tmpA1.next;
                tmpB1 = tmpB1.next;
            } 
            return null;

        }
    }
  • 环形链表II:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    /**
     * Definition for singly-linked list.
     * class ListNode {
     *     int val;
     *     ListNode next;
     *     ListNode(int x) {
     *         val = x;
     *         next = null;
     *     }
     * }
     */
    public class Solution {
        public ListNode detectCycle(ListNode head) {
            // 定义一个hashmap
            HashMap<Integer, ListNode> map = new HashMap<>();
            // 定义一个虚拟头节点
            ListNode dummy = new ListNode(0);
            dummy.next = head;
            // 定义索引
            int index = 0;

            // 循环
            while (dummy.next!=null){
                if (map.containsValue(dummy)){
                    return dummy;
                }else{
                    map.put(index, dummy);
                    index++;
                    dummy = dummy.next;
                }
            }
            return null;
        }
    }

4. 数组

4.1 读取数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import java.io.*;

public class Main{
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        // 如果第一行表示节点个数，那就读取n
        int n = Integer.parseInt(reader.readLine());
        String[] s = reader.readLine().split(" "); //用空格分割，也可以用逗号分割

        int[] nums = new int[s.length];
        for (int i = 0; i < s.length; i++){
            nums[i] = Integer.parseInt(s[i]);
        }

        // 关闭资源
        reader.close();
    }
}

4.2 访问元素

1
2
3
4
5
/* 访问元素 */
int access(int[] nums, int index) {
    // 获取并返回随机元素
    return nums[index];
}

4.3 插入元素

1
2
3
4
5
6
7
8
9
/* 在数组的索引 index 处插入元素 num */
void insert(int[] nums, int num, int index) {
    // 把索引 index 以及之后的所有元素向后移动一位
    for (int i = nums.length - 1; i > index; i--) {
        nums[i] = nums[i - 1];
    }
    // 将 num 赋给 index 处元素
    nums[index] = num;
}

4.4 删除元素

1
2
3
4
5
6
7
/* 删除索引 index 处元素 */
void remove(int[] nums, int index) {
    // 把索引 index 之后的所有元素向前移动一位
    for (int i = index; i < nums.length - 1; i++) {
        nums[i] = nums[i + 1];
    }
}

4.5 遍历数组

1
2
3
4
5
6
7
8
9
10
11
12
/* 遍历数组 */
void traverse(int[] nums) {
    int count = 0;
    // 通过索引遍历数组
    for (int i = 0; i < nums.length; i++) {
        count++;
    }
    // 直接遍历数组
    for (int num : nums) {
        count++;
    }
}c

4.6 查找元素

1
2
3
4
5
6
7
8
/* 在数组中查找指定元素 */
int find(int[] nums, int target) {
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] == target)
            return i;
    }
    return -1;
}

4.7 扩容数组

1
2
3
4
5
6
7
8
9
10
11
/* 扩展数组长度 */
int[] extend(int[] nums, int enlarge) {
    // 初始化一个扩展长度后的数组
    int[] res = new int[nums.length + enlarge];
    // 将原数组中的所有元素复制到新数组
    for (int i = 0; i < nums.length; i++) {
        res[i] = nums[i];
    }
    // 返回扩展后的新数组
    return res;
}

4.8 模板题

  • 二分查找:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    class Solution {
        public int search(int[] nums, int target) {
            // 左
            int left = 0;
            // 右
            int right = nums.length - 1;
            while (left<=right){
                // 中间
                int middle = left + (right - left) / 2;
                if (nums[middle]>target){
                    right = middle - 1;
                } else if (nums[middle] < target) {
                    left = middle + 1;
                }else {
                    return middle;
                }
            }
            return -1;
        }
    }

  • 移除元素:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    class Solution {
        public int removeElement(int[] nums, int val) {
            // 1. 定义两个指针fast, slow
            int slow = 0;
            for (int fast=0; fast<=nums.length-1; fast++){
                if (nums[fast] != val){
                    nums[slow++] = nums[fast];
                }
            }
            return slow;
        }
    }

  • 有序数组的平方:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    class Solution {
        public int[] sortedSquares(int[] nums) {
            // 双向双指针
            int left = 0;
            int right = nums.length - 1;
            int index = nums.length - 1;
            int[] result = new int[nums.length];
            while (left <= right){
                if (nums[right]*nums[right] > nums[left]*nums[left]){
                    result[index--] = nums[right]*nums[right];
                    right--;
                }else{
                    result[index--] = nums[left]*nums[left];
                    left++;
                }
            }
            return result;
        }
    }

  • 长度最小的子数组:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    class Solution {
        public int minSubArrayLen(int target, int[] nums) {
            int left = 0;
            int sum = 0;
            int len = Integer.MAX_VALUE;
            for (int right=0; right<nums.length; right++){
                sum += nums[right];
                while (sum>=target){
                    len = Math.min(len, right-left+1);
                    sum -= nums[left++];
                }
            }
            return len == Integer.MAX_VALUE ? 0 : len;

        }
    }

  • 螺旋矩阵II:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    class Solution {
        public int[][] generateMatrix(int n) {
            // 定义左右上下
            int left = 0, right = n-1, top = 0, bottom = n-1;
            // 定义填充的总数和正填充的计数
            int count = 1, target = n*n;
            // 定义返回的数组
            int[][] returnList = new int[n][n];

            // i表示遍历行，j表示遍历列
            while (count<=target){
                // 从左到右
                for (int j=left; j<=right; j++){
                    returnList[top][j] = count++;
                }
                top++;
                // 从上往下
                for (int i=top; i<=bottom; i++){
                    returnList[i][right] = count++;
                }
                right--;
                // 从右往左
                for (int j=right; j>=left; j--){
                    returnList[bottom][j] = count++;
                }
                bottom--;
                // 从下往上
                for (int i=bottom; i>=top; i--){
                    returnList[i][left] = count++;
                }
                left++;
            }
            return returnList;
        }
    }

5. 栈

5.1 基本操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/* 初始化栈 */
Stack<Integer> stack = new Stack<>();

/* 元素入栈 */
stack.push(1);
stack.push(2);

/* 访问栈顶元素 */
int peek = stack.peek();

/* 元素出栈 */
int pop = stack.pop();

/* 获取栈的长度 */
int size = stack.size();

/* 判断是否为空 */
boolean isEmpty = stack.isEmpty();

5.2 基于链表实现栈

  • push：链表头插法
  • pop：删除头节点
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    /* 基于链表实现的栈 */
    class LinkedListStack {
        private ListNode stackPeek; // 将头节点作为栈顶
        private int stkSize = 0; // 栈的长度

        public LinkedListStack() {
            stackPeek = null;
        }

        /* 获取栈的长度 */
        public int size() {
            return stkSize;
        }

        /* 判断栈是否为空 */
        public boolean isEmpty() {
            return size() == 0;
        }

        /* 入栈 */
        public void push(int num) {
            ListNode node = new ListNode(num);
            node.next = stackPeek;
            stackPeek = node;
            stkSize++;
        }

        /* 出栈 */
        public int pop() {
            int num = peek();
            stackPeek = stackPeek.next;
            stkSize--;
            return num;
        }

        /* 访问栈顶元素 */
        public int peek() {
            if (size() == 0)
                throw new IndexOutOfBoundsException();
            return stackPeek.val;
        }

        /* 将 List 转化为 Array 并返回 */
        public int[] toArray() {
            ListNode node = stackPeek;
            int[] res = new int[size()];
            for (int i = res.length - 1; i >= 0; i--) {
                res[i] = node.val;
                node = node.next;
            }
            return res;
        }
    }

5.3 基于数组实现栈

  • push：插入到数组尾部
  • pop：删除数组尾元素
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    /* 基于数组实现的栈 */
    class ArrayStack {
        private ArrayList<Integer> stack;

        public ArrayStack() {
            // 初始化列表（动态数组）
            stack = new ArrayList<>();
        }

        /* 获取栈的长度 */
        public int size() {
            return stack.size();
        }

        /* 判断栈是否为空 */
        public boolean isEmpty() {
            return size() == 0;
        }

        /* 入栈 */
        public void push(int num) {
            stack.add(num);
        }

        /* 出栈 */
        public int pop() {
            if (isEmpty())
                throw new IndexOutOfBoundsException();
            return stack.remove(size() - 1);
        }

        /* 访问栈顶元素 */
        public int peek() {
            if (isEmpty())
                throw new IndexOutOfBoundsException();
            return stack.get(size() - 1);
        }

        /* 将 List 转化为 Array 并返回 */
        public Object[] toArray() {
            return stack.toArray();
        }
    }

5.4 模板题

  • 用栈实现队列:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    class MyQueue {
        // 定义两个栈
        Stack<Integer> stackIn;
        Stack<Integer> stackOut;

        // 构造函数
        public MyQueue() {
            stackIn = new Stack<>();
            stackOut = new Stack<>();
        }
        
        // 入队列
        public void push(int x) {
            stackIn.push(x);
        }
        
        // 出队列
        public int pop() {
            dumpstackIn();
            return stackOut.pop();
        }
        
        // 返回队列开头元素
        public int peek() {
            dumpstackIn();
            return stackOut.peek();
        }
        
        // 判断队列是否为空
        public boolean empty() {
            return stackIn.isEmpty() & stackOut.isEmpty();
        }

        // 如果stackOut为空，那么将stackIn中的元素全部放到stackOut中
        public void dumpstackIn(){
            // 出队列：判断stackOut是否为空，不为空就返回
            if (!stackOut.isEmpty())return;
            while (!stackIn.isEmpty()){
                stackOut.push(stackIn.pop());
            }
        }
    }

  • 用队列实现栈:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    class MyStack {
        // 定义两个队列
        Queue<Integer> queue1;
        Queue<Integer> queue2;

        // 构造器
        public MyStack() {
            queue1 = new LinkedList<>();
            queue2 = new LinkedList<>(); 
        }
        
        // 入栈流程是：
        // 入栈元素放入queue2中
        // 然后将queue1元素全部放入queue2中
        // 最后queue1和queue2互换
        public void push(int x) {
            queue2.offer(x); // 先放在辅助队列中
            while (!queue1.isEmpty()){
                queue2.offer(queue1.poll());
            }
            Queue<Integer> queueTemp;
            queueTemp = queue1;
            queue1 = queue2;
            queue2 = queueTemp; // 最后交换queue1和queue2，将元素都放到queue1中
        }
        
        // 出栈
        // queue2
        public int pop() {
            return queue1.poll();
        }
        
        // 返回栈顶元素
        public int top() {
            return queue1.peek();
        }
        
        // 判断是否为空
        public boolean empty() {
            return queue1.isEmpty();
        }
    }

  • 有效的括号:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    class Solution {
        public boolean isValid(String s) {
            // if (s.length()%2!=0) return false;

            // 定义一个栈
            Stack<Character> stack = new Stack<>();

            // 循环
            for (int i=0; i<=s.length()-1; i++){
                if (s.charAt(i) == '('){
                    stack.push(')');
                }else if (s.charAt(i) == '{'){
                    stack.push('}');
                }else if (s.charAt(i) == '['){
                    stack.push(']');
                }else if (stack.isEmpty() || stack.peek()!=s.charAt(i)){
                    return false;
                }else {
                    stack.pop();
                }
                
            }
            return stack.isEmpty();
        }
    }

  • 删除字符串中的所有相邻重复项:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    class Solution {
        public String removeDuplicates(String s) {
            Stack<Character> stack = new Stack<>();
            Stack<Character> stack1 = new Stack<>();

            for (int i=0; i<=s.length()-1; i++){
                if (stack.isEmpty() || stack.peek()!=s.charAt(i)){
                    stack.push(s.charAt(i));
                }else{
                    stack.pop();
                }
            }
            StringBuilder sb = new StringBuilder();
            while (!stack.isEmpty()){
                stack1.push(stack.pop());
            }
            while (!stack1.isEmpty()){
                sb.append(stack1.pop());
            }
            return sb.toString();
        }
    }

  • 逆波兰表达式求值:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    class Solution {
        public int evalRPN(String[] tokens) {
            // 1. 定义一个栈
            Stack<Integer> stack = new Stack<>();
            // 2. 定义运算的两个变量
            int a;
            int b;

            // 3. 对tokens进行遍历
            for (String s : tokens){
                if (s.equals("+")){
                    b = stack.pop();
                    a = stack.pop();
                    stack.push(a+b);
                }else if (s.equals("-")){
                    b = stack.pop();
                    a = stack.pop();
                    stack.push(a-b);
                }else if (s.equals("*")){
                    b = stack.pop();
                    a = stack.pop();
                    stack.push(a*b);
                }else if (s.equals("/")){
                    b = stack.pop();
                    a = stack.pop();
                    stack.push(a/b);
                }else{
                    stack.push(Integer.valueOf(s));
                }
            }
            return stack.peek();
        }
    }

  • 滑动窗口最大值:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    class Solution {
        public int[] maxSlidingWindow(int[] nums, int k) {
            if(nums.length == 0 || k == 0) return new int[0];
            Deque<Integer> deque = new LinkedList<>();
            int[] res = new int[nums.length - k + 1];
            for(int j = 0, i = 1 - k; j < nums.length; i++, j++) {
                // 删除 deque 中对应的 nums[i-1]
                if(i > 0 && deque.peekFirst() == nums[i - 1])
                    deque.removeFirst();
                // 保持 deque 递减
                while(!deque.isEmpty() && deque.peekLast() < nums[j])
                    deque.removeLast();
                deque.addLast(nums[j]);
                // 记录窗口最大值
                if(i >= 0)
                    res[i] = deque.peekFirst();
            }
            return res;
        }
    }

  • 前 K 个高频元素:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    class Solution {
        public int[] topKFrequent(int[] nums, int k) {
            // 优先级队列，为了避免复杂 api 操作，pq 存储数组
            // lambda 表达式设置优先级队列从大到小存储 o1 - o2 为从大到小，o2 - o1 反之
            PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
            int[] res = new int[k]; // 答案数组为 k 个元素
            Map<Integer, Integer> map = new HashMap<>(); // 记录元素出现次数
            for(int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);
            for(var x : map.entrySet()) { // entrySet 获取 k-v Set 集合
                // 将 kv 转化成数组
                int[] tmp = new int[2];
                tmp[0] = x.getKey();
                tmp[1] = x.getValue();
                pq.offer(tmp);
                if(pq.size() > k) {
                    pq.poll();
                }
            }
            for(int i = 0; i < k; i ++) {
                res[i] = pq.poll()[0]; // 获取优先队列里的元素
            }
            return res;
        }
    }

6. 队列

6.1 队列常用操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/* 初始化队列 */
Queue<Integer> queue = new LinkedList<>();

/* 元素入队 */
queue.offer(1);
queue.offer(2);

/* 访问队首元素 */
int peek = queue.peek();

/* 元素出队 */
int pop = queue.poll();

/* 获取队列的长度 */
int size = queue.size();

/* 判断队列是否为空 */
boolean isEmpty = queue.isEmpty();

6.2 基于链表实现队列

  • push：添加到链表尾部
  • pop：删除链表头节点
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    /* 基于链表实现的队列 */
    class LinkedListQueue {
        private ListNode front, rear; // 头节点 front ，尾节点 rear
        private int queSize = 0;

        public LinkedListQueue() {
            front = null;
            rear = null;
        }

        /* 获取队列的长度 */
        public int size() {
            return queSize;
        }

        /* 判断队列是否为空 */
        public boolean isEmpty() {
            return size() == 0;
        }

        /* 入队 */
        public void push(int num) {
            // 尾节点后添加 num
            ListNode node = new ListNode(num);
            // 如果队列为空，则令头、尾节点都指向该节点
            if (front == null) {
                front = node;
                rear = node;
            // 如果队列不为空，则将该节点添加到尾节点后
            } else {
                rear.next = node;
                rear = node;
            }
            queSize++;
        }

        /* 出队 */
        public int pop() {
            int num = peek();
            // 删除头节点
            front = front.next;
            queSize--;
            return num;
        }

        /* 访问队首元素 */
        public int peek() {
            if (size() == 0)
                throw new IndexOutOfBoundsException();
            return front.val;
        }

        /* 将链表转化为 Array 并返回 */
        public int[] toArray() {
            ListNode node = front;
            int[] res = new int[size()];
            for (int i = 0; i < res.length; i++) {
                res[i] = node.val;
                node = node.next;
            }
            return res;
        }
    }

6.3 双向队列常用操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/* 初始化双向队列 */
Deque<Integer> deque = new LinkedList<>();

/* 元素入队 */
deque.offerLast(1);   // 添加至队尾
deque.offerFirst(3);  // 添加至队首

/* 访问元素 */
int peekFirst = deque.peekFirst();  // 队首元素
int peekLast = deque.peekLast();    // 队尾元素

/* 元素出队 */
int popFirst = deque.pollFirst();  // 队首元素出队
int popLast = deque.pollLast();    // 队尾元素出队

/* 获取双向队列的长度 */
int size = deque.size();

/* 判断双向队列是否为空 */
boolean isEmpty = deque.isEmpty();

6.4 基于双向链表实现双向队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
/* 双向链表节点 */
class ListNode {
    int val; // 节点值
    ListNode next; // 后继节点引用
    ListNode prev; // 前驱节点引用

    ListNode(int val) {
        this.val = val;
        prev = next = null;
    }
}

/* 基于双向链表实现的双向队列 */
class LinkedListDeque {
    private ListNode front, rear; // 头节点 front ，尾节点 rear
    private int queSize = 0; // 双向队列的长度

    public LinkedListDeque() {
        front = rear = null;
    }

    /* 获取双向队列的长度 */
    public int size() {
        return queSize;
    }

    /* 判断双向队列是否为空 */
    public boolean isEmpty() {
        return size() == 0;
    }

    /* 入队操作 */
    private void push(int num, boolean isFront) {
        ListNode node = new ListNode(num);
        // 若链表为空，则令 front, rear 都指向 node
        if (isEmpty())
            front = rear = node;
        // 队首入队操作
        else if (isFront) {
            // 将 node 添加至链表头部
            front.prev = node;
            node.next = front;
            front = node; // 更新头节点
        // 队尾入队操作
        } else {
            // 将 node 添加至链表尾部
            rear.next = node;
            node.prev = rear;
            rear = node; // 更新尾节点
        }
        queSize++; // 更新队列长度
    }

    /* 队首入队 */
    public void pushFirst(int num) {
        push(num, true);
    }

    /* 队尾入队 */
    public void pushLast(int num) {
        push(num, false);
    }

    /* 出队操作 */
    private Integer pop(boolean isFront) {
        // 若队列为空，直接返回 null
        if (isEmpty())
            return null;
        int val;
        // 队首出队操作
        if (isFront) {
            val = front.val; // 暂存头节点值
            // 删除头节点
            ListNode fNext = front.next;
            if (fNext != null) {
                fNext.prev = null;
                front.next = null;
            }
            front = fNext; // 更新头节点
        // 队尾出队操作
        } else {
            val = rear.val; // 暂存尾节点值
            // 删除尾节点
            ListNode rPrev = rear.prev;
            if (rPrev != null) {
                rPrev.next = null;
                rear.prev = null;
            }
            rear = rPrev; // 更新尾节点
        }
        queSize--; // 更新队列长度
        return val;
    }

    /* 队首出队 */
    public Integer popFirst() {
        return pop(true);
    }

    /* 队尾出队 */
    public Integer popLast() {
        return pop(false);
    }

    /* 访问队首元素 */
    public Integer peekFirst() {
        return isEmpty() ? null : front.val;
    }

    /* 访问队尾元素 */
    public Integer peekLast() {
        return isEmpty() ? null : rear.val;
    }

    /* 返回数组用于打印 */
    public int[] toArray() {
        ListNode node = front;
        int[] res = new int[size()];
        for (int i = 0; i < res.length; i++) {
            res[i] = node.val;
            node = node.next;
        }
        return res;
    }
}

7. 哈希表

7.1 哈希表常用操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/* 初始化哈希表 */
Map<Integer, String> map = new HashMap<>();

/* 添加操作 */
// 在哈希表中添加键值对 (key, value)
map.put(12836, "小哈");   
map.put(15937, "小啰");   
map.put(16750, "小算");   
map.put(13276, "小法");
map.put(10583, "小鸭");

/* 查询操作 */
// 向哈希表输入键 key ，得到值 value
String name = map.get(15937);

/* 删除操作 */
// 在哈希表中删除键值对 (key, value)
map.remove(10583);

/* 遍历哈希表 */
// 遍历键值对 key->value
for (Map.Entry <Integer, String> kv: map.entrySet()) {
    System.out.println(kv.getKey() + " -> " + kv.getValue());
}
// 单独遍历键 key
for (int key: map.keySet()) {
    System.out.println(key);
}
// 单独遍历值 value
for (String val: map.values()) {
    System.out.println(val);
}

8. 树

8.1 二叉树

  • 二叉树常见术语：

    • 根节点 root node：位于二叉树顶层的节点，没有父节点。
    • 叶节点 leaf node：没有子节点的节点，其两个指针均指向。
    • 边 edge：连接两个节点的线段，即节点引用（指针）。
    • 节点所在的层 level：从顶至底递增，根节点所在层为 1 。
    • 节点的度 degree：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。
    • 二叉树的高度 height：从根节点到最远叶节点所经过的边的数量。
    • 节点的深度 depth：从根节点到该节点所经过的边的数量。
    • 节点的高度 height：从最远叶节点到该节点所经过的边的数量。

  • 二叉树分类：

    • 完美二叉树（满二叉树）
    • 完全二叉树
    • 完满二叉树
    • 平衡二叉树

  • 二叉树基本操作

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
      /* 二叉树节点类 */
      class TreeNode {
          int val;         // 节点值
          TreeNode left;   // 左子节点引用
          TreeNode right;  // 右子节点引用
          TreeNode(int x) { val = x; }
      }

      /* 初始化二叉树 */
      // 初始化节点
      TreeNode n1 = new TreeNode(1);
      TreeNode n2 = new TreeNode(2);
      TreeNode n3 = new TreeNode(3);
      TreeNode n4 = new TreeNode(4);
      TreeNode n5 = new TreeNode(5);
      // 构建引用指向（即指针）
      n1.left = n2;
      n1.right = n3;
      n2.left = n4;
      n2.right = n5;
      
      /* 插入与删除节点 */
      TreeNode P = new TreeNode(0);
      // 在 n1 -> n2 中间插入节点 P
      n1.left = P;
      P.left = n2;
      // 删除节点 P
      n1.left = n2;
      ```  
      ![](面试-算法/树_2.png)

    - 读取二叉树：
      ```java
      import java.io.BufferedReader;
      import java.io.IOException;
      import java.io.InputStreamReader;
       
      public class Main{
          //4.输入二叉树
          public static void main(String[] args) throws IOException {
              //获取键盘一行的输入，以enter键为结束标志
              BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
              String[] s = reader.readLine().split(" "); //用空格分割，也可以用逗号分割
       
              //用数组按层级遍历顺序存储二叉树的节点
              TreeNode[] tree = new TreeNode[s.length];
              for(int i = 0; i < tree.length; i++){
                  int val_i = Integer.parseInt(s[i]);
                  if(val_i == -1){
                      tree[i] = null; //-1代表null
                  }else{
                      tree[i] = new TreeNode(val_i); 
                  }
              }
       
              //再遍历一边，给左右子树赋值
              for(int i = 0; i * 2 + 2 < tree.length; i++){
                  if(tree[i] != null){
                      tree[i].left = tree[i * 2 + 1];
                      tree[i].right = tree[i * 2 + 2];
                  }
              }
              TreeNode root = tree[0];
              //root是最终得到的二叉树根节点
          }
       
          //辅助类：构造树需要的结点类
          static class TreeNode {
              int val;
              TreeNode left, right;
              public TreeNode(int val) {
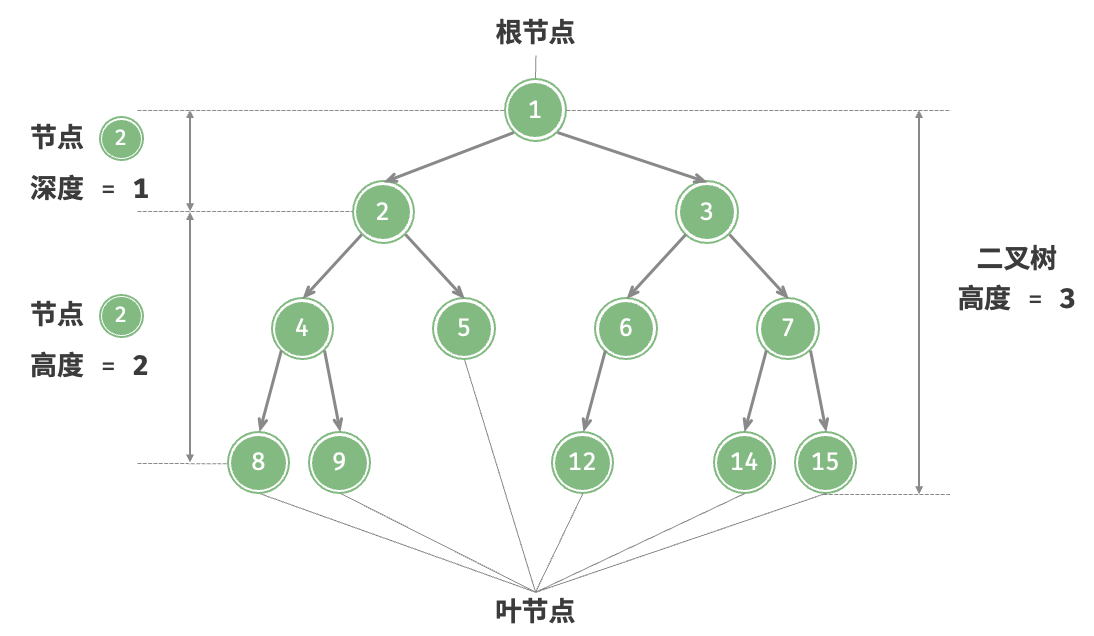
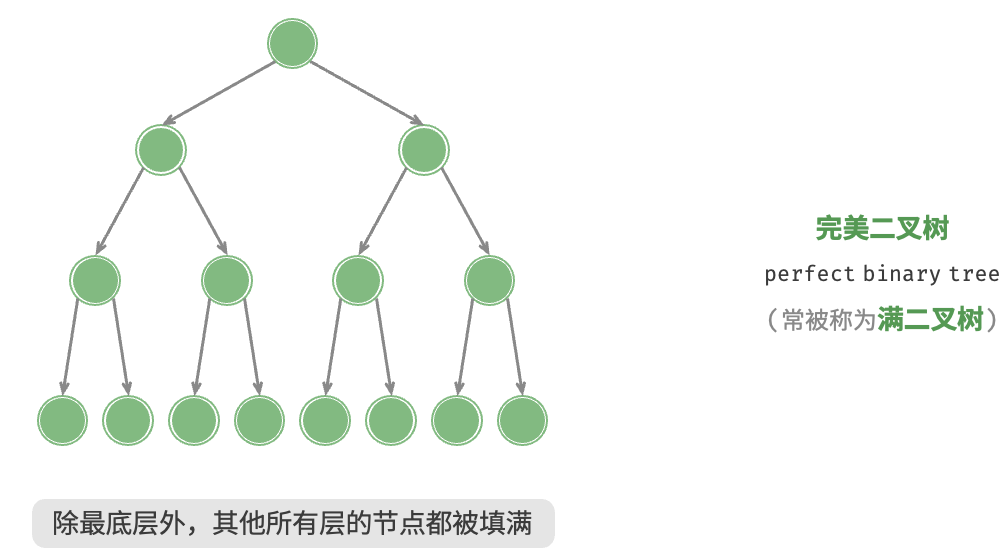
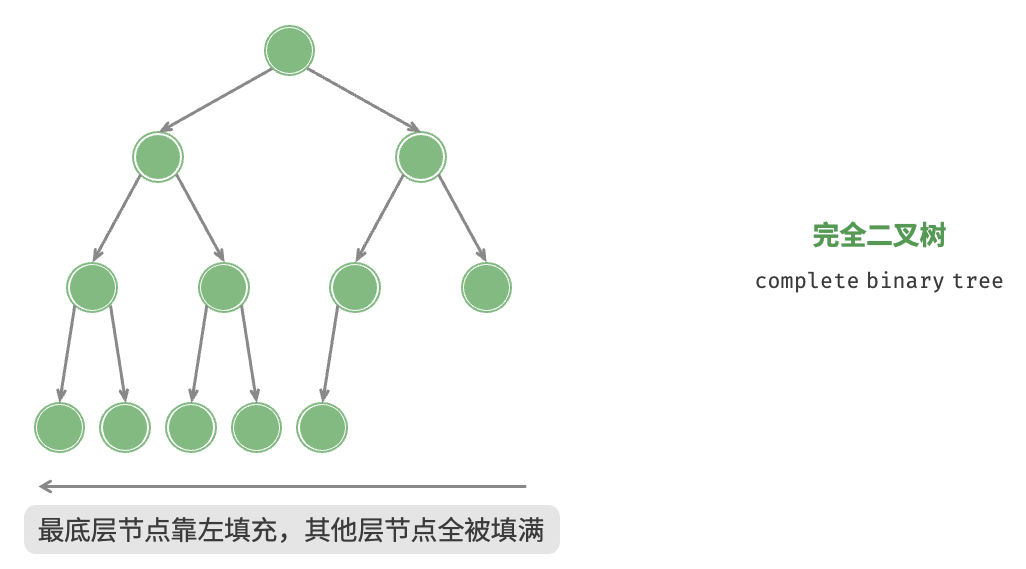
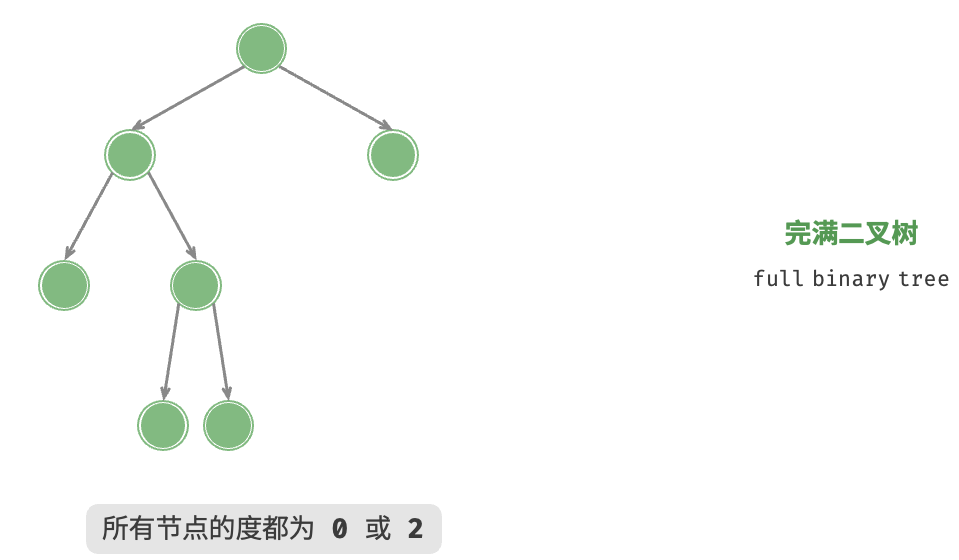
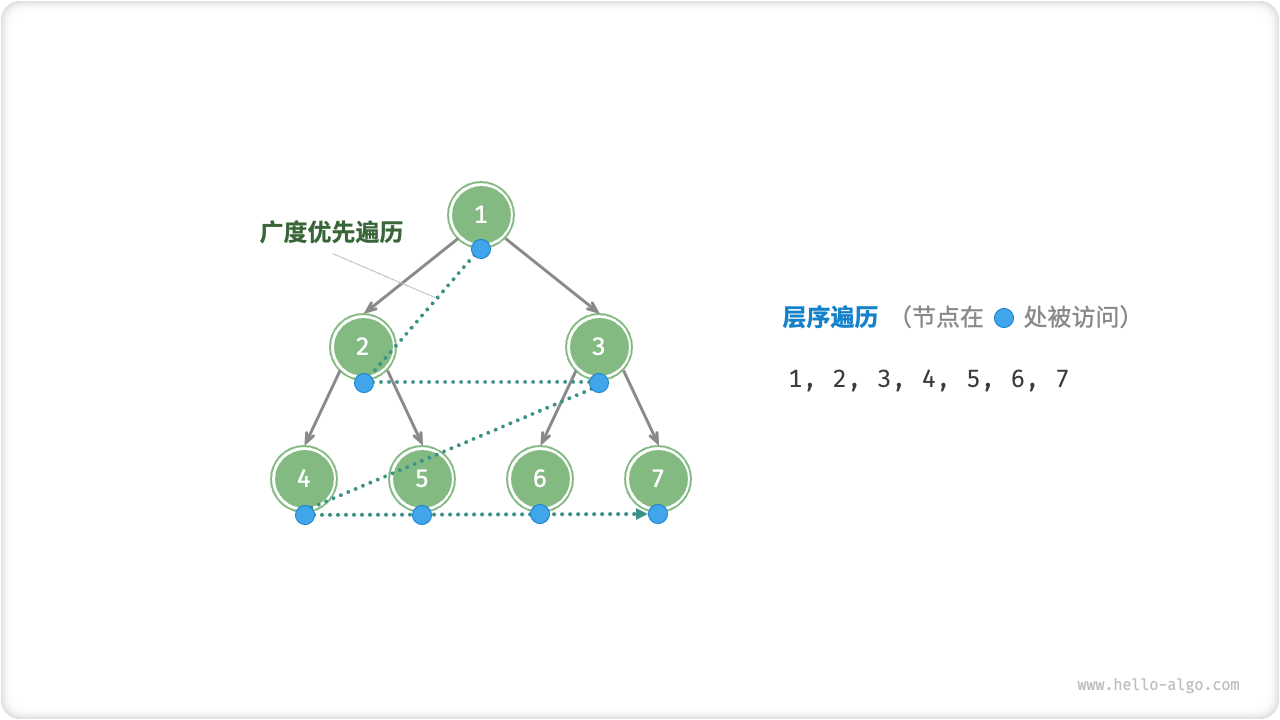
                  this.val = val;
              }
          }
      }

8.2 二叉树遍历

  • 层序遍历：本质上属于广度优先遍历 breadth-first traversal，它体现了一种“一圈一圈向外扩展”的逐层遍历方式。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    /* 层序遍历 */
    List<Integer> levelOrder(TreeNode root) {
        // 初始化队列，加入根节点
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        // 初始化一个列表，用于保存遍历序列
        List<Integer> list = new ArrayList<>();
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll(); // 队列出队
            list.add(node.val);           // 保存节点值
            if (node.left != null){
                queue.offer(node.left);   // 左子节点入队
            }
            if (node.right != null){
                queue.offer(node.right);  // 右子节点入队
            }
        }
        return list;
    }
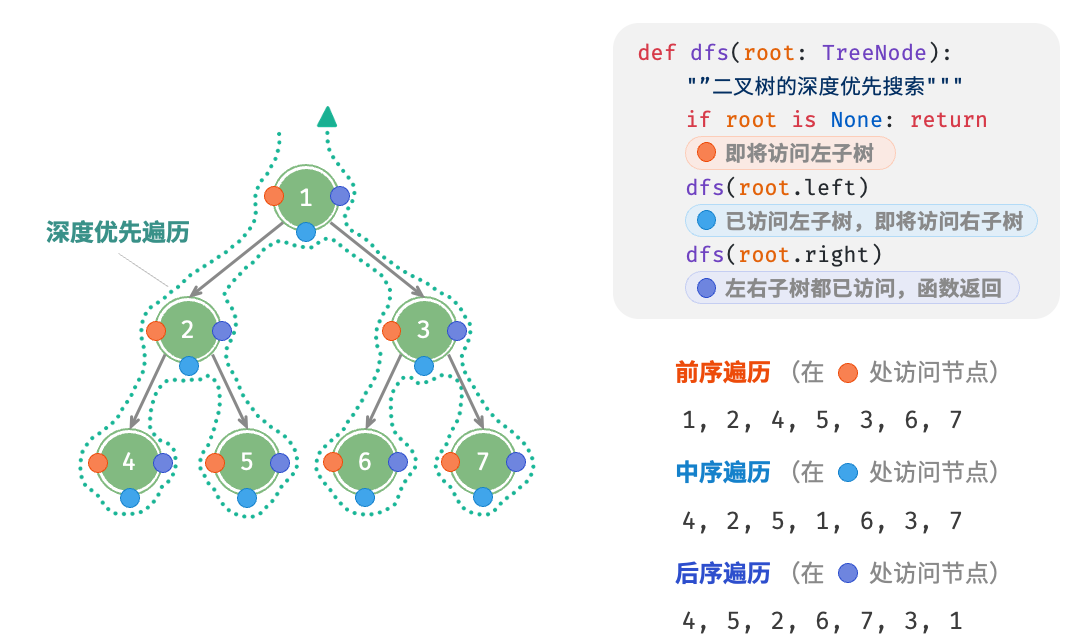
  • 前序、中序、后序遍历：都属于「深度优先遍历 depth-first traversal」，它体现了一种“先走到尽头，再回溯继续”的遍历方式。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    /* 前序遍历 */
    void preOrder(TreeNode root) {
        if (root == null)
            return;
        // 访问优先级：根节点 -> 左子树 -> 右子树
        list.add(root.val);
        preOrder(root.left);
        preOrder(root.right);
    }

    /* 中序遍历 */
    void inOrder(TreeNode root) {
        if (root == null)
            return;
        // 访问优先级：左子树 -> 根节点 -> 右子树
        inOrder(root.left);
        list.add(root.val);
        inOrder(root.right);
    }

    /* 后序遍历 */
    void postOrder(TreeNode root) {
        if (root == null)
            return;
        // 访问优先级：左子树 -> 右子树 -> 根节点
        postOrder(root.left);
        postOrder(root.right);
        list.add(root.val);
    }

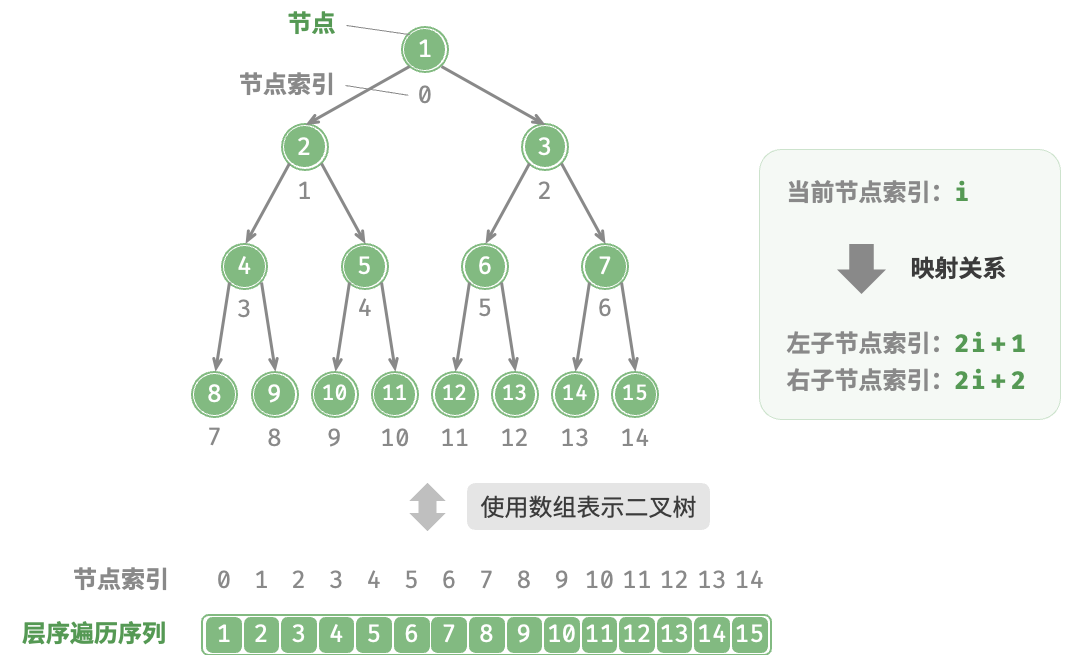
8.3 二叉树数组表示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
/* 数组表示下的二叉树类 */
class ArrayBinaryTree {
    private List<Integer> tree;

    /* 构造方法 */
    public ArrayBinaryTree(List<Integer> arr) {
        tree = new ArrayList<>(arr);
    }

    /* 节点数量 */
    public int size() {
        return tree.size();
    }

    /* 获取索引为 i 节点的值 */
    public Integer val(int i) {
        // 若索引越界，则返回 null ，代表空位
        if (i < 0 || i >= size())
            return null;
        return tree.get(i);
    }

    /* 获取索引为 i 节点的左子节点的索引 */
    public Integer left(int i) {
        return 2 * i + 1;
    }

    /* 获取索引为 i 节点的右子节点的索引 */
    public Integer right(int i) {
        return 2 * i + 2;
    }

    /* 获取索引为 i 节点的父节点的索引 */
    public Integer parent(int i) {
        return (i - 1) / 2;
    }

    /* 层序遍历 */
    public List<Integer> levelOrder() {
        List<Integer> res = new ArrayList<>();
        // 直接遍历数组
        for (int i = 0; i < size(); i++) {
            if (val(i) != null)
                res.add(val(i));
        }
        return res;
    }

    /* 深度优先遍历 */
    private void dfs(Integer i, String order, List<Integer> res) {
        // 若为空位，则返回
        if (val(i) == null)
            return;
        // 前序遍历
        if (order == "pre")
            res.add(val(i));
        dfs(left(i), order, res);
        // 中序遍历
        if (order == "in")
            res.add(val(i));
        dfs(right(i), order, res);
        // 后序遍历
        if (order == "post")
            res.add(val(i));
    }

    /* 前序遍历 */
    public List<Integer> preOrder() {
        List<Integer> res = new ArrayList<>();
        dfs(0, "pre", res);
        return res;
    }

    /* 中序遍历 */
    public List<Integer> inOrder() {
        List<Integer> res = new ArrayList<>();
        dfs(0, "in", res);
        return res;
    }

    /* 后序遍历 */
    public List<Integer> postOrder() {
        List<Integer> res = new ArrayList<>();
        dfs(0, "post", res);
        return res;
    }
}

8.4 二叉搜索树

  • 二叉搜索树(binary search tree)满足以下条件：

    • 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
    • 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1. 。

  • 查找节点

    • 若 cur.val < num ，说明目标节点在 cur 的右子树中，因此执行 cur = cur.right 。
    • 若 cur.val > num ，说明目标节点在 cur 的左子树中，因此执行 cur = cur.left 。
    • 若 cur.val = num ，说明找到目标节点，跳出循环并返回该节点。
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      /* 查找节点 */
      TreeNode search(int num) {
          TreeNode cur = root;
          // 循环查找，越过叶节点后跳出
          while (cur != null) {
              // 目标节点在 cur 的右子树中
              if (cur.val < num)
                  cur = cur.right;
              // 目标节点在 cur 的左子树中
              else if (cur.val > num)
                  cur = cur.left;
              // 找到目标节点，跳出循环
              else
                  break;
          }
          // 返回目标节点
          return cur;
      }

  • 插入节点

    • 查找插入位置：与查找操作相似，从根节点出发，根据当前节点值和 num 的大小关系循环向下搜索，直到越过叶节点（遍历至None）时跳出循环。
    • 在该位置插入节点：初始化节点 num ，将该节点插入当前的位置。
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      /* 插入节点 */
      void insert(int num) {
          // 若树为空，则初始化根节点
          if (root == null) {
              root = new TreeNode(num);
              return;
          }
          TreeNode cur = root, pre = null;
          // 循环查找，越过叶节点后跳出
          while (cur != null) {
              // 找到重复节点，直接返回
              if (cur.val == num)
                  return;
              pre = cur;
              // 插入位置在 cur 的右子树中
              if (cur.val < num)
                  cur = cur.right;
              // 插入位置在 cur 的左子树中
              else
                  cur = cur.left;
          }
          // 插入节点
          TreeNode node = new TreeNode(num);
          if (pre.val < num)
              pre.right = node;
          else
              pre.left = node;
      }

  • 删除节点：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    /* 删除节点 */
    void remove(int num) {
        // 若树为空，直接提前返回
        if (root == null)
            return;
        TreeNode cur = root, pre = null;
        // 循环查找，越过叶节点后跳出
        while (cur != null) {
            // 找到待删除节点，跳出循环
            if (cur.val == num)
                break;
            pre = cur;
            // 待删除节点在 cur 的右子树中
            if (cur.val < num)
                cur = cur.right;
            // 待删除节点在 cur 的左子树中
            else
                cur = cur.left;
        }
        // 若无待删除节点，则直接返回
        if (cur == null)
            return;
        // 子节点数量 = 0 or 1
        if (cur.left == null || cur.right == null) {
            // 当子节点数量 = 0 / 1 时， child = null / 该子节点
            TreeNode child = cur.left != null ? cur.left : cur.right;
            // 删除节点 cur
            if (cur != root) {
                if (pre.left == cur)
                    pre.left = child;
                else
                    pre.right = child;
            } else {
                // 若删除节点为根节点，则重新指定根节点
                root = child;
            }
        }
        // 子节点数量 = 2
        else {
            // 获取中序遍历中 cur 的下一个节点
            TreeNode tmp = cur.right;
            while (tmp.left != null) {
                tmp = tmp.left;
            }
            // 递归删除节点 tmp
            remove(tmp.val);
            // 用 tmp 覆盖 cur
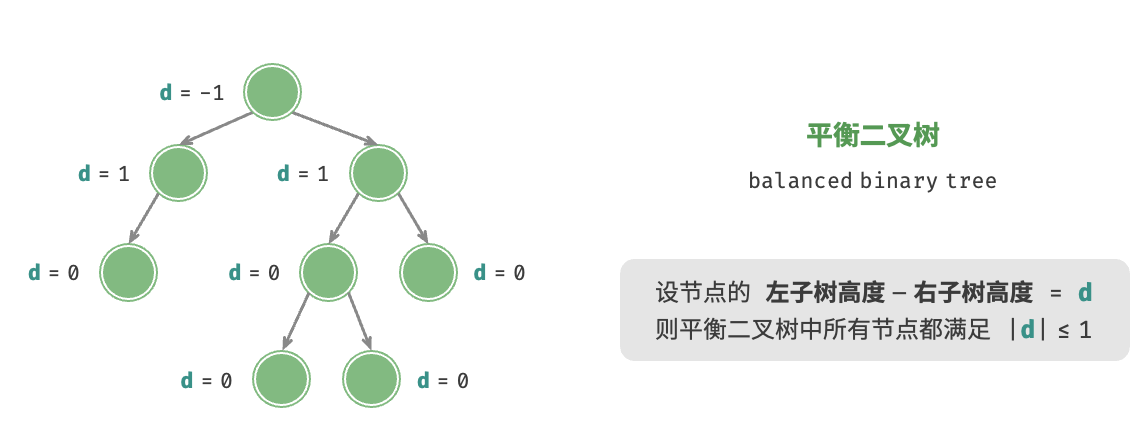
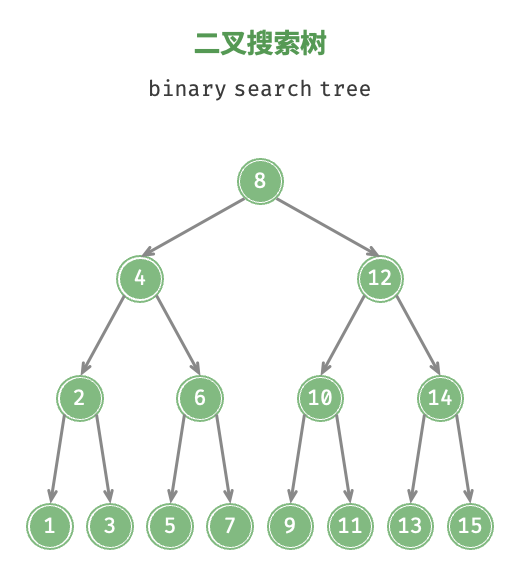
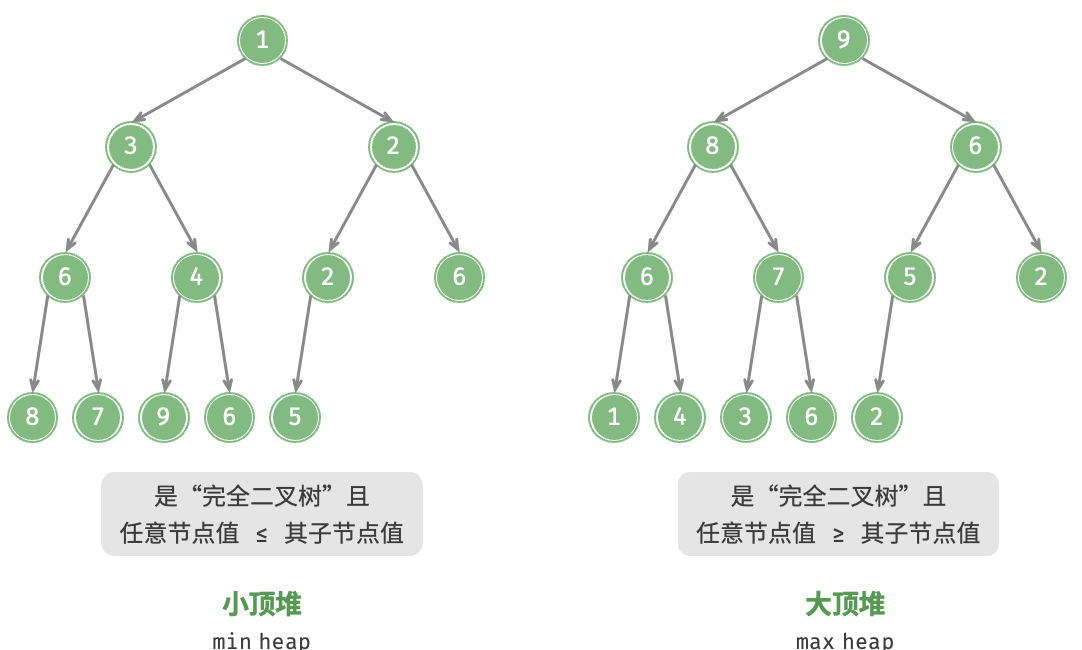
            cur.val = tmp.val;
        }
    }

8.5 AVL树

9. 堆

9.1 基础问题

  • 概念：

    • 大顶堆 max heap：任意节点的值大于等于其子节点的值。
    • 小顶堆 min heap：任意节点的值小于等于其子节点的值。

  • 堆常用操作:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    /* 初始化堆 */
    // 初始化小顶堆
    Queue<Integer> minHeap = new PriorityQueue<>();
    // 初始化大顶堆（使用 lambda 表达式修改 Comparator 即可）
    Queue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);

    /* 元素入堆 */
    maxHeap.offer(1);
    maxHeap.offer(3);
    maxHeap.offer(2);
    maxHeap.offer(5);
    maxHeap.offer(4);

    /* 获取堆顶元素 */
    int peek = maxHeap.peek(); // 5

    /* 堆顶元素出堆 */
    // 出堆元素会形成一个从大到小的序列
    peek = maxHeap.poll(); // 5
    peek = maxHeap.poll(); // 4
    peek = maxHeap.poll(); // 3
    peek = maxHeap.poll(); // 2
    peek = maxHeap.poll(); // 1

    /* 获取堆大小 */
    int size = maxHeap.size();

    /* 判断堆是否为空 */
    boolean isEmpty = maxHeap.isEmpty();

    /* 输入列表并建堆 */
    minHeap = new PriorityQueue<>(Arrays.asList(1, 3, 2, 5, 4));

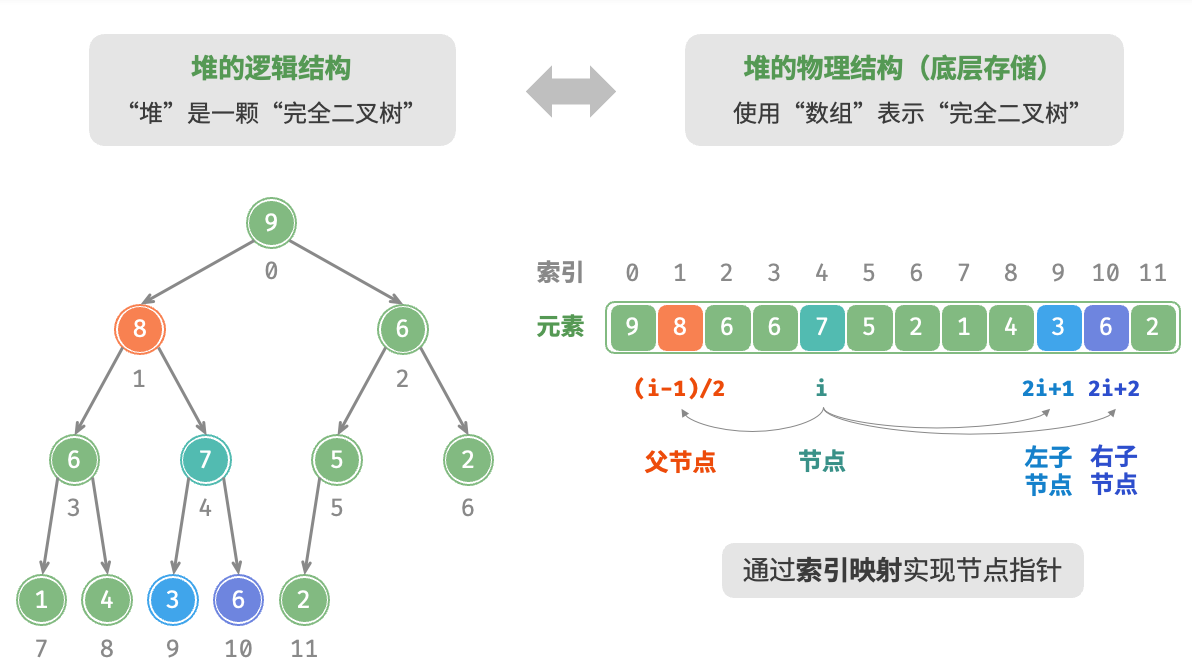
9.2 建堆操作

  • 堆的存储与表示：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
/* 获取左子节点索引 */
int left(int i) {
    return 2 * i + 1;
}

/* 获取右子节点索引 */
int right(int i) {
    return 2 * i + 2;
}

/* 获取父节点索引 */
int parent(int i) {
    return (i - 1) / 2; // 向下整除
}

/* 访问堆顶元素 */
int peek() {
    return maxHeap.get(0);
}

/* 元素入堆 */
void push(int val) {
    // 添加节点
    maxHeap.add(val);
    // 从底至顶堆化
    siftUp(size() - 1);
}

/* 从节点 i 开始，从底至顶堆化 */
void siftUp(int i) {
    while (true) {
        // 获取节点 i 的父节点
        int p = parent(i);
        // 当“越过根节点”或“节点无须修复”时，结束堆化
        if (p < 0 || maxHeap.get(i) <= maxHeap.get(p))
            break;
        // 交换两节点
        swap(i, p);
        // 循环向上堆化
        i = p;
    }
}

/* 元素出堆 */
int pop() {
    // 判空处理
    if (isEmpty())
        throw new IndexOutOfBoundsException();
    // 交换根节点与最右叶节点（即交换首元素与尾元素）
    swap(0, size() - 1);
    // 删除节点
    int val = maxHeap.remove(size() - 1);
    // 从顶至底堆化
    siftDown(0);
    // 返回堆顶元素
    return val;
}

/* 从节点 i 开始，从顶至底堆化 */
void siftDown(int i) {
    while (true) {
        // 判断节点 i, l, r 中值最大的节点，记为 ma
        int l = left(i), r = right(i), ma = i;
        if (l < size() && maxHeap.get(l) > maxHeap.get(ma))
            ma = l;
        if (r < size() && maxHeap.get(r) > maxHeap.get(ma))
            ma = r;
        // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if (ma == i)
            break;
        // 交换两节点
        swap(i, ma);
        // 循环向下堆化
        i = ma;
    }
}


9.3 Top-K 问题

  • 给定一个长度为无序数组nums，请返回数组中前 k 大的元素。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    /* 基于堆查找数组中最大的 k 个元素 */
    Queue<Integer> topKHeap(int[] nums, int k) {
        Queue<Integer> heap = new PriorityQueue<Integer>();
        // 将数组的前 k 个元素入堆
        for (int i = 0; i < k; i++) {
            heap.offer(nums[i]);
        }
        // 从第 k+1 个元素开始，保持堆的长度为 k
        for (int i = k; i < nums.length; i++) {
            // 若当前元素大于堆顶元素，则将堆顶元素出堆、当前元素入堆
            if (nums[i] > heap.peek()) {
                heap.poll();
                heap.offer(nums[i]);
            }
        }
        return heap;
    }

10. 图

10.1 基于邻接矩阵的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
/* 基于邻接矩阵实现的无向图类 */
class GraphAdjMat {
    List<Integer> vertices; // 顶点列表，元素代表“顶点值”，索引代表“顶点索引”
    List<List<Integer>> adjMat; // 邻接矩阵，行列索引对应“顶点索引”

    /* 构造方法 */
    public GraphAdjMat(int[] vertices, int[][] edges) {
        this.vertices = new ArrayList<>();
        this.adjMat = new ArrayList<>();
        // 添加顶点
        for (int val : vertices) {
            addVertex(val);
        }
        // 添加边
        // 请注意，edges 元素代表顶点索引，即对应 vertices 元素索引
        for (int[] e : edges) {
            addEdge(e[0], e[1]);
        }
    }

    /* 获取顶点数量 */
    public int size() {
        return vertices.size();
    }

    /* 添加顶点 */
    public void addVertex(int val) {
        int n = size();
        // 向顶点列表中添加新顶点的值
        vertices.add(val);
        // 在邻接矩阵中添加一行
        List<Integer> newRow = new ArrayList<>(n);
        for (int j = 0; j < n; j++) {
            newRow.add(0);
        }
        adjMat.add(newRow);
        // 在邻接矩阵中添加一列
        for (List<Integer> row : adjMat) {
            row.add(0);
        }
    }

    /* 删除顶点 */
    public void removeVertex(int index) {
        if (index >= size())
            throw new IndexOutOfBoundsException();
        // 在顶点列表中移除索引 index 的顶点
        vertices.remove(index);
        // 在邻接矩阵中删除索引 index 的行
        adjMat.remove(index);
        // 在邻接矩阵中删除索引 index 的列
        for (List<Integer> row : adjMat) {
            row.remove(index);
        }
    }

    /* 添加边 */
    // 参数 i, j 对应 vertices 元素索引
    public void addEdge(int i, int j) {
        // 索引越界与相等处理
        if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
            throw new IndexOutOfBoundsException();
        // 在无向图中，邻接矩阵沿主对角线对称，即满足 (i, j) == (j, i)
        adjMat.get(i).set(j, 1);
        adjMat.get(j).set(i, 1);
    }

    /* 删除边 */
    // 参数 i, j 对应 vertices 元素索引
    public void removeEdge(int i, int j) {
        // 索引越界与相等处理
        if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
            throw new IndexOutOfBoundsException();
        adjMat.get(i).set(j, 0);
        adjMat.get(j).set(i, 0);
    }

    /* 打印邻接矩阵 */
    public void print() {
        System.out.print("顶点列表 = ");
        System.out.println(vertices);
        System.out.println("邻接矩阵 =");
        PrintUtil.printMatrix(adjMat);
    }
}

10.2 基于邻接表的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
/* 基于邻接表实现的无向图类 */
class GraphAdjList {
    // 邻接表，key: 顶点，value：该顶点的所有邻接顶点
    Map<Vertex, List<Vertex>> adjList;

    /* 构造方法 */
    public GraphAdjList(Vertex[][] edges) {
        this.adjList = new HashMap<>();
        // 添加所有顶点和边
        for (Vertex[] edge : edges) {
            addVertex(edge[0]);
            addVertex(edge[1]);
            addEdge(edge[0], edge[1]);
        }
    }

    /* 获取顶点数量 */
    public int size() {
        return adjList.size();
    }

    /* 添加边 */
    public void addEdge(Vertex vet1, Vertex vet2) {
        if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
            throw new IllegalArgumentException();
        // 添加边 vet1 - vet2
        adjList.get(vet1).add(vet2);
        adjList.get(vet2).add(vet1);
    }

    /* 删除边 */
    public void removeEdge(Vertex vet1, Vertex vet2) {
        if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
            throw new IllegalArgumentException();
        // 删除边 vet1 - vet2
        adjList.get(vet1).remove(vet2);
        adjList.get(vet2).remove(vet1);
    }

    /* 添加顶点 */
    public void addVertex(Vertex vet) {
        if (adjList.containsKey(vet))
            return;
        // 在邻接表中添加一个新链表
        adjList.put(vet, new ArrayList<>());
    }

    /* 删除顶点 */
    public void removeVertex(Vertex vet) {
        if (!adjList.containsKey(vet))
            throw new IllegalArgumentException();
        // 在邻接表中删除顶点 vet 对应的链表
        adjList.remove(vet);
        // 遍历其他顶点的链表，删除所有包含 vet 的边
        for (List<Vertex> list : adjList.values()) {
            list.remove(vet);
        }
    }

    /* 打印邻接表 */
    public void print() {
        System.out.println("邻接表 =");
        for (Map.Entry<Vertex, List<Vertex>> pair : adjList.entrySet()) {
            List<Integer> tmp = new ArrayList<>();
            for (Vertex vertex : pair.getValue())
                tmp.add(vertex.val);
            System.out.println(pair.getKey().val + ": " + tmp + ",");
        }
    }
}

10.3 图的遍历

  • 广度优先遍历：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    /* 广度优先遍历 BFS */
    // 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
    List<Vertex> graphBFS(GraphAdjList graph, Vertex startVet) {
        // 顶点遍历序列
        List<Vertex> res = new ArrayList<>();
        // 哈希表，用于记录已被访问过的顶点
        Set<Vertex> visited = new HashSet<>();
        visited.add(startVet);
        // 队列用于实现 BFS
        Queue<Vertex> que = new LinkedList<>();
        que.offer(startVet);
        // 以顶点 vet 为起点，循环直至访问完所有顶点
        while (!que.isEmpty()) {
            Vertex vet = que.poll(); // 队首顶点出队
            res.add(vet);            // 记录访问顶点
            // 遍历该顶点的所有邻接顶点
            for (Vertex adjVet : graph.adjList.get(vet)) {
                if (visited.contains(adjVet))
                    continue;        // 跳过已被访问过的顶点
                que.offer(adjVet);   // 只入队未访问的顶点
                visited.add(adjVet); // 标记该顶点已被访问
            }
        }
        // 返回顶点遍历序列
        return res;
    }

  • 深度优先遍历：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    /* 深度优先遍历 DFS 辅助函数 */
    void dfs(GraphAdjList graph, Set<Vertex> visited, List<Vertex> res, Vertex vet) {
        res.add(vet);     // 记录访问顶点
        visited.add(vet); // 标记该顶点已被访问
        // 遍历该顶点的所有邻接顶点
        for (Vertex adjVet : graph.adjList.get(vet)) {
            if (visited.contains(adjVet))
                continue; // 跳过已被访问过的顶点
            // 递归访问邻接顶点
            dfs(graph, visited, res, adjVet);
        }
    }

    /* 深度优先遍历 DFS */
    // 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
    List<Vertex> graphDFS(GraphAdjList graph, Vertex startVet) {
        // 顶点遍历序列
        List<Vertex> res = new ArrayList<>();
        // 哈希表，用于记录已被访问过的顶点
        Set<Vertex> visited = new HashSet<>();
        dfs(graph, visited, res, startVet);
        return res;
    }

10.4 拓扑排序

11. 搜索

12. 分治

13. 回溯算法

14. 动态规划

15. 贪心算法

wxzhouJava Development

个人简介。